Archives for "April, 2011"
Written methods of multiplication
In our Four Rules, Multiplication category we have a range of pages which look at written methods of multiplication. Parents seem to have been confused by what is taught in school, but it is really the process leading up to the standard written method which has changed: the standard method itself is very much the [...]
What maths should children know by the end of Year 5?
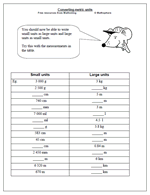
Much of the work carried out in year 4 eg addition and subtraction is reinforced in year 5. Efficient written methods for all addition, subtraction and multiplication are expected and moving towards this with division. Please note that this is only a summary of the key areas of maths to be covered in the year. [...]
Adding fractions with totals more than one.
One of the hardest things to get across to children is how to add fractions. All too often they will just add the numerator (top number of the fraction) and denominator (bottom number of the fraction) and get the wrong answer. The key to success is to create two equivalent fractions with the same denominator. [...]
Year 5: converting metric units
Just a quick exercise in converting metric units from small to large and vice versa. This is not easy and as stated before a good understanding of both the metric system and place value is needed to be able to do this. It is probably easier to convert large units to smaller: Eg 3.5 litres [...]
7 times table practice
I have had several requests for more in the way of tables practice sheets: so here is one for the 7 times table. The 7 times table is probably the hardest of the lot as there is little in the way of a recognisable pattern in the digits. However, if 2, 3, 4, 5 6 [...]
What maths should children know by the end of Year 4?
Now we have come to what is expected of children aged between 8 and 9: as defined by the English Primary Framework for Mathematics (part of the National Curriculum). In year 4 there is a greater emphasis on written methods, with the standard or efficient method expected for both addition and subtraction. Children are expected [...]
Maths worksheets on Knowing Multiplication Facts in year 6
Expectations of what children should know are high in Year 6 but we have a great selection of maths worksheets to help. It is assumed (often wrongly) that by Year 6 children have a good knowledge of ‘tables’ and can quickly recall any table from 2 to 10. With this in mind they can put [...]
6 SATs practice questions
This is the first in my series of ‘Booster’ worksheets for year 6 children who are about to take the SAT tests. They aim to boost a child’s score in the test papers by making them familiar with the types of questions that they will come across. It is rare for a straightforward sum of [...]
Year 4 quite hard mental subtraction
Many children are unaware that there are often several ways of working out a calculation and that those who choose the best methods find maths easier and are able to answer questions more quickly and more accurately. Let’s look at ‘Subtract 38 from 63. This should be done, ‘in your head’ and will involve several [...]
Written subtraction of 3-digits (2)
Written subtraction is one of those areas of maths that children frequently get wrong, mainly because they do not fully understand the method. This page looks at 3-digit subtraction and all the questions need ‘decomposition’ in order to get them correct. The last three questions should be laid out in the same way as the [...]
- © 2009 Maths Blog
- Privacy Policy