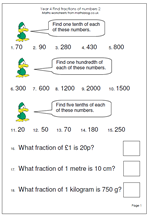
Whilst most of the mathsblog site gives away free worksheets I do have a small selection of fun maths games for reception/Year 1 children. Counting is a major part of maths iat this age and by the end of reception should be able to say and use number names up to 10. A good example of this would be to join in nursery rhymes or songs such as
“One, two three, four, five. Once I caught a fish alive.”
Children should also be counting up in ones, up to 10 objects. This would be in a practical sense of counting a number of objects that they can touch (pieces of a jigsaw, coins, hats etc). Later they can count things they can see, but not touch (panes in a window, cows in a field etc ).They can then begin to count down from a small number e.g. 5,4,3,2,1,0.
We have a great set of fun maths games on counting for Reception/Early Years and one of my particular favourites is the Counting Goats game. This is really good practice at counting up to 5. Young children can not get too much practice with this both in the home and on the computer. They may well use their fingers to help and count out loud, but after a time they will begin to count in their heads. Adults can often glimpse at a picture to see how many there are, almost without counting – don’t expect this of 5 a year old! Don’t forget to click on the banjo playing goat at the end for a happy tune!
We have a great set of counting games, so why not have a go today?
Go to our Counting games
If you like these games why not have a free trial of urbrainy.com, which has many, many more?
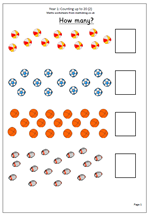 It is often assumed that children in year 1 are capable at counting, but this is frequently not the case and they need plenty of practice reciting the number names and counting on and back.
It is often assumed that children in year 1 are capable at counting, but this is frequently not the case and they need plenty of practice reciting the number names and counting on and back.