Free Year 4 Maths Worksheets | Maths Blog

Maths Worksheet: Year 4 Find a Difference

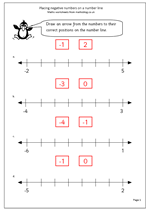
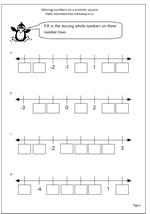
Sometimes a simple question can reveal a great deal about how children deal with numbers. This maths worksheet on finding differences is full of such questions.

Let’s look at 3005 – 8 which is easier to do mentally than on paper.

There are several ways that this can be done.

1. Count down, one at a time, 8 from 3005, saying each number as you go. Fingers may be held up on each count down until 8 is reached.

3004, (1), 3003 (2), 3002 (3), 3001 (4), 3000 (5), 2999 (6), 2998 (7), 2997 (8)

2. A different way is to take the 8 from 3000, then add 5.

3000 – 8 = 2992

2992 + 5 = 2997

3. A third way is to take 5 off the 8 leaving 3.

Then take 3 off 3000 = 2997

It is well worth talking to children about how they do this kind of question and what strategies they employ. Much will depend on their knowledge of number.

Find a difference by counting up (pg 1)

Maths Worksheet: Year 4 Order Decimal Fractions

$order-decimal-fractions-y4-p1$ It is important that children recognise that the value of a digit depends on its place in the number – otherwise we could only possibly have 9 numbers and zero! So the digit 1 in 120 has a different value than the 1 in 210. It is, of course ten times bigger as it is 100 rather than 10.

By Year 4 children should be applying this idea to decimals. The first column to the right of the decimal point is tenths so the 1 in 2.1 has a value of one tenth.

This maths worksheets looks at both place value and ordering simple decimal fractions. Children probably come across decimal fractions more often with money than any other area and it is a really good way to show place value eg one penny is £0.01, or one hundredth, whilst 10p is £0.10 or one tenth of a pound. (Notice we always put two digits after the decimal when using money, but not at other times.)

Order decimal fractions y4 p1

Maths Worksheet: Decimal Fractions, tenths

$decimal-fractions-tenths-pg1$ Fractions and decimals are two of the sticking points in maths, but here we have a maths worksheet which neatly combines the two, showing the equivalence between fractions and decimal fractions. Many children do not realise the link between a digit written after the decimal point and a fraction i.e. 0.2 is the same as 2/10.

One way to show this is to use the fraction as a division sum. 2/10 can be seen as 2 divided by 10. Do this on a calculator to get 0.2. Also remember, to divide by ten mentally, just move each digit one place to the right, putting in the decimal point if moving from units to tenths.

Decimal fractions: tenths (pg1)

Year 4 Maths worksheet: Find fractions of numbers

$year4-find-fractions-2$ This worksheet looks at the relationship between fractions and division. It is important that children understand that finding one half of a number is equivalent to dividing by 2, that finding one quarter of a number is the same as dividing the number by 4 and to find one fifth is equivalent to dividing by 5. Plenty of practice is needed with this before children go on to find, for example, two fifths, or three fifths of numbers.
Most of these questions should be calculated mentally, although rough jottings may help. It might be a help to remember that finding a quarter of a number can be found by halving and then halving again. A fifth can be found by dividing by ten and doubling the answer, although if the number is not divisible by 10 it might be easier to do a quick pencil and paper calculation.

Find fractions of numbers (p2)

Year 4 number worksheet: recognising tests of divisibility for 4 and 5

There are some things which children can learn which can really help them later at High School. Tests of divisibility are a great set of ‘tricks’ to know and will certainly help any child with their maths in the future. This page looks at divisibility by 4 and 5. Being divisible by 5 means that there is no remainder when a number is divided by 5; in other words it divides exactly.

Recognising when a number is divisible by 5 is easy: only whole numbers ending in 5 or 0 are divisible by 5.

Recognising a number which is divisible by 4 is harder: are the last two digits divisible by 4? If so then the number is too. eg 156344 is divisible by 4. (try it with a calculator.)

This worksheet only uses 2-digit numbers which by year 4 children should be able to divide by 4 in their heads. (Halve and halve again: if the answer is a whole number it is divisible by 4).

Divisible by 4 and 5

Mental arithmetic: Subtracting single digits from multiples of 100 and 1000

A pretty straightforward worksheet in two parts. The first part looks at subtraction of a single digit from multiples of 100. The second half looks at subtracting from multiples of 1000. The obvious way to do this is to count back, but when you ask children who are very quick with maths they seem to employ other tactics with little to do with subtraction. For example, one 9 year old boy told me his explanation of 8000 – 6:

‘turn the 800 into 799 and add 4 to make the next whole ten. Answer 7994’

Not the clearest explanation ever, but it seems that he is doing a kind of decomposition in his head – interesting!

Subtract from multiples of 100 or 1000

Year 4 maths worksheet: Placing negative numbers

This worksheet takes another look at negative numbers and where they are positioned on a number line. This is a good exercise in helping children to count back through zero and then from a negative number forwards, again through zero. Each number line has a different starting and finishing number so care needs to be taken.Try to use the term ‘negative’ rather than ‘minus’ when referring to the numbers.

Place negative numbers on a number line (pg 1)

Year 4 Maths worksheet: negative numbers

Negative numbers become an important part of maths in Year 4. Usually the best way to teach it is through practical work such as the use of thermometers when the temperature drops below zero. Whilst temperature is read using the term ‘minus’ it is a good idea to read negative numbers as ‘negative 3’ or ‘negative 5’.

There are 2 ideas at work here. Firstly, understanding the idea of numbers smaller than zero can be tricky. Children might ask how you can have a number smaller than nothing. An overdraft is always a good starting point to explain this! Also the idea that a larger digit can portray a smaller number eg -6 is smaller than -1.

This maths worksheet uses number lines that go from left to right, from a negative number through zero to positive numbers.

Order negative numbers pg 1

Year 4 maths worksheet: multiplying by 10 and 100

Understanding what happens when you multiply a whole number by 10 is crucial to understanding maths at primary school and indeed with later maths. Children should have carried out lots of practical work with base 10 apparatus in school to show that:

when you multiply a whole number by 10 the digits move one place to the left.

Now this may give the appearance of ‘adding a nought’ as a zero is placed in the units. I know of many teachers and publishers who still use this expression, but it is extremely dangerous, especially when it comes to multiplying decimals by 10. (0.8 is not 0.80).

Multiplying by 100 is the same as multiplying by 10 and then multiplying by 10 again (10 x 10 = 100) so each digit will move two places to the left and zeros will need to be placed in the units and tens.

When you multiply a whole number by 100 the digits move two places to the left.

Multiplying by 10 and 100 (pg 1)

Year 4 Maths number worksheet: Half way between

Finding the number which lies half way between two other numbers can be easy or quite tricky, even when using fairly small numbers. When using whole tens or hundreds the questions tend to be quite straightforward, as does finding halfway between two consecutive whole numbers. Most of the questions on this number worksheet are of this easier type. One of the harder questions here is to find half way between 20 and 80 and it is interesting to ask how people go about this mentally. Often they will conduct a mental process of adding ten to the lower number and subtracting ten from the higher number until they meet ‘in the middle’.

Half way between pg 1