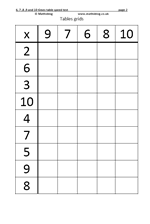
This is the second page for tables 6 to 10. The idea is to fill in the grid as quickly as possible. The tens are easy, although never suggest that ‘add a naught’ will give the correct answer! The nines are interesting in that the digits have a digital root of 9 when added (1 + 8 = 9, 2 + 7 = 9 etc). The six, seven and eight times tables are probably the hardest for most children to learn.
When completing the grid various tactics can be used if the tables have not been thoroughly learned. For example, 6 x 9 is just 6 less than 6 x 10; 7 x 9 is 7 less than 7 x 10 etc.
Also if they know that 6 x 7 = 42 then use this to answer 7 x 6, which will also be 42.
However, the ultimate aim is to know tables off by heart.
Year 1 worksheets: Counting up to 20
Here we have a very straightforward couple of pages with up to 20 sweets to count. We work hard with children when they first start to count but then tend to neglect this area of counting on past ten. The sweets have been laid out in such a way that there are rows of ten. ‘Bright sparks’ may spot this and start at ten and just count the second row. ‘Burning hot’ sparks might do a quick subtraction with the rows that are nearly ten: it’s always interesting to watch how children set about tasks such as these.
There’s lots more for young children at urbrainy.com, which is rapidly becoming one of the best sites around for early years maths.
Year 5 Maths worksheet: More equivalent fractions
Here we have some more work on understanding equivalence in fractions.
The first question looks at simple equivalence between halves, fifths, tenths etc and asks which fractions are less than a half. The quick way to work this out is to see if the top number (numerator) is less than double the bottom number (denominator) – if it is then it is less than one half.
The second question requires an understanding that a fraction such as four fifths can be changed to an equivalent fraction such as eight tenths by multiplying both the numerator and denominator by the same number (in this case 2, but it will not always be 2). All the fractions need to be changed to the same denominator which in this case would be 30.
The other questions are all aimed at improving understanding of equivalence.
Maths worksheet: Long division
Perhaps the hardest thing that children are asked to do in primary school is long division – and many children never master it, not even later in life. The main reason it is so difficult is that involves a number of stages, a good knowledge of tables and multiplication as well as subtraction. Looking at a problem such as 867 divided by 34, there are at least ten distinctive stages to go through:
34)867
First carry out an estimate of the answer. I think 867 divided by 34 is over 20 but under 30.
Then proceed using these steps:
1. How many 34s in 86?
2. 2 x 34 is 68. 3 x 34 is 102 which is too many, so it must be 2.
3. Put the 2 in the tens column above the answer.
4. Place the 68 below the 86 and subtract.
5. 86 – 68 is 18.
6. ‘Bring down’ the 7 to make 187.
7. How many 34s in 187.
8. By trial and improvement and some rough work multiplying 34 by my estimated numbers I find that 34 x 5 = 170.
9. Place the 170 under the 187 and subtract.
10. The remainder must be less than the original number you are dividing by.
Maths worksheet: Standard subtraction of 3-digits
Here is a basic set of subtraction questions using 3-digit numbers. They should be tackled in the standard method as described in earlier 2-digit subtraction worksheets. Notice that there are no zeros in the tens column as this can lead to particular problems and needs a set of questions all of its own.
The last three questions have been set out in a horizontal form. To answer them they should be rewritten in the standard way. Look out for mistakes where decomposition was needed but where the subtraction has been reversed eg 3 – 7 has been done as 7 – 3.
If these questions are answered correctly and in the correct method then it can be said that mastery of the subtraction method is well on its way!
Coming soon: long division, equivalent fractions and tables
Some pretty meaty stuff coming during the next week or so, including the standard method of long division. Many children never master long division, with good reason, as they need to be proficient in multiplication, tables and mental subtraction to succeed. We also have some equivalent fractions for Year 5 and the standard or efficient method for subtraction for 3-digit numbers. Also coming soon is another page for practising the 6, 7, 8, 9 and 10 times tables. For younger children there are pages on Counting up to 20.
Year 4 number worksheet: recognising tests of divisibility for 4 and 5
There are some things which children can learn which can really help them later at High School. Tests of divisibility are a great set of ‘tricks’ to know and will certainly help any child with their maths in the future. This page looks at divisibility by 4 and 5. Being divisible by 5 means that there is no remainder when a number is divided by 5; in other words it divides exactly.
Recognising when a number is divisible by 5 is easy: only whole numbers ending in 5 or 0 are divisible by 5.
Recognising a number which is divisible by 4 is harder: are the last two digits divisible by 4? If so then the number is too. eg 156344 is divisible by 4. (try it with a calculator.)
This worksheet only uses 2-digit numbers which by year 4 children should be able to divide by 4 in their heads. (Halve and halve again: if the answer is a whole number it is divisible by 4).
Understand relationships between addition, subtraction, multiplication and division
Not many questions on this page but an impressive number of maths concepts needed to answer the questions correctly. These include:
Understanding that addition can be done in any order so: 50 + 15 = 15 + 50
Understanding that 45 – 31 is different from 31 – 45
Understanding that addition reverses subtraction, ie addition is the inverse of subtraction
Understanding that division reverses multiplication, ie division is the inverse of multiplication
Understanding that 16 ÷ 8 does not equal 8 ÷ 16
Begin to understand the commutative law (although not the term)
Example of the commutative law: 24 x 12 = 12 x 24
If a child has cracked all these ideas they are well on the way to success.
Understand relationships between addition, subtraction, multiplication and division
Year 2 maths worksheet: finding halves (pg 2)
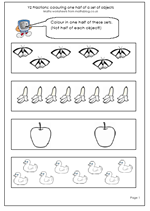The third in our mini series of fraction maths worksheets. This looks again at halves and finding half of a set of objects, keeping to small, even numbers. The best way to re-inforce this work is to carry out practical activities, dividing groups of objects into two equal groups – make sure you keep to an even starting number. Sweets, marbles, lego bricks etc are ideal for this.
Mental arithmetic: Subtracting single digits from multiples of 100 and 1000
A pretty straightforward worksheet in two parts. The first part looks at subtraction of a single digit from multiples of 100. The second half looks at subtracting from multiples of 1000. The obvious way to do this is to count back, but when you ask children who are very quick with maths they seem to employ other tactics with little to do with subtraction. For example, one 9 year old boy told me his explanation of 8000 – 6:
‘turn the 800 into 799 and add 4 to make the next whole ten. Answer 7994’
Not the clearest explanation ever, but it seems that he is doing a kind of decomposition in his head – interesting!