By far the best the best maths equipment that I have come across over the years is the Stern Structural Arithmetic programme, which encourages children to reason rather than just rote learn. This approach was designed to follow a child’s natural stages of learning and development in the early years upward, to develop a number sense, number knowledge, concepts and number relationships, as well as ensuring that the pre-requisite skills are soundly in place prior to any formal work. It is also ideal for SEN children where little or no progress has been made in the past and for children who have been ‘moved on’ to the next stage, clearly before understanding the earlier stages.
Stimulating a child’s cognitive processing functions sits at the heart of the programme; the range of equipment provides wonderful ‘pictures’ which develop visual and auditory perceptual processing.
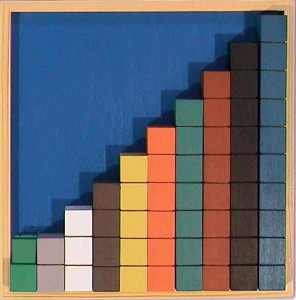
One example is the ‘stair’ in the 10-Box, where adding one more cube makes it the same ‘size’ as the next number. The concept then is explicit – adding one to any number will always result in the next number.
The Counting Board introduces position and sequence. The simple task, when asked to find a block to fit into an empty groove indicated, naturally develops a child’s judging, scanning and discrimination ability. Children discover that each block has its own special place in the series of blocks to 10. This means that it is not necessary only to work with numbers to 5. Number relationships are a vital building block. Instead, children see the small numbers all ‘live’ at the beginning, and bigger ones ‘live’ at the end, (later to become on the left/right).
As an example of the Structural Arithmetic approach, look at 3 + 7 = 10. Children discover all the combinations that make 10 by fitting combinations of blocks into the 10-box. They reason that if 9 needs 1 to make 10, then 8 needs 2, and 7 needs 3 to make 10. By switching the blocks around, they discover that the order of the addends can be changed without changing the sum. Thus, they grasp that addition can be done in any order and can put it to use, reasoning that if 7 + 3 = 10, then 3 + 7 = 10. This fact has not been learned in isolation, but has been studied in a context where its relatioship to the other facts can be seen.
When children see an example such as 5 + 4 = and don’t know the answer, they often respond by counting “6, 7, 8, 9.” Teachers may assume that encouraging children to count, will one day result in their stopping counting and saying, ‘9’. Stern argues that, in fact, each time they see + 4 (as in 6 + 4 or 9 + 4), they automatically practise counting. The numbers themselves don’t have meaning. For the counting child, 5 plus 4 does not equal 9; it makes 9 by counting. No picture in the child’s mind makes the number fact 5 + 4 = 9 unforgettable. Furthermore, if children count the total incorrectly as 10, they have no certain way to check that result except by another uncertain counting procedure. On the other hand, in Structural Arithmetic, the two addends 5 and 4 actually measure 9 in the Number Track.
The Stern kits are not cheap, but I would recommend having a further read at
http://www.mathsextra.com/





 When working out how many more to make a number up to 100 it is important not to mix up two different ways of doing it. Let’s take the question:
When working out how many more to make a number up to 100 it is important not to mix up two different ways of doing it. Let’s take the question: